This package creates possible distributions based on reported sample parameters, using the SPRITE algorithm. This can be used to check what the original sample might have looked like, and thus to understand the data generation process better. This can help with the identification of fabricated data or misreported parameters, but also with checking whether sample characteristics such as floor/ceiling effects might suggest that findings are spurious.
For that, it implements the SPRITE algorithm proposed by Heathers et al. (2018). Much of the code for is based on Nick Brown’s rSPRITE shiny app, with some extensions. If you are just interested in interactive use and do not need these extensions (see advanced usage below) that Shiny online app (see https://shiny.ieis.tue.nl/sprite/) might be better for you.
The package also includes dedicated functions to run the GRIM and GRIMMER tests. GRIM_test() checks whether a reported mean based on integers is consistent with a given sample size, while GRIMMER_test() checks whether a reported standard deviation is consistent with a reported mean and sample size. They can help catch impossible distributions and reporting errors without running any simulations.
Installation
rsprite2 can be installed from CRAN with:
install.packages("rsprite2")Or you might want to install the development version from GitHub:
install.packages("remotes")
remotes::install_github('LukasWallrich/rsprite2')Simple example
To create possible distributions, SPRITE needs the reported mean, standard deviation, sample size and range of values.
For instance, what distribution of 20 responses on a 1 to 5 scale might result in a mean of 2.2 and a standard deviation of 1.3?
library(rsprite2)
sprite_parameters <- set_parameters(mean = 2.2, sd = 1.3, n_obs = 20, min_val = 1, max_val = 5)
find_possible_distribution(sprite_parameters)
#> $outcome
#> [1] "success"
#>
#> $values
#> [1] 2 2 2 4 2 1 1 4 1 1 2 1 4 2 5 1 4 2 3 1
#>
#> $mean
#> [1] 2.25
#>
#> $sd
#> [1] 1.292692
#>
#> $iterations
#> [1] 4If these means and standard deviations had been reported to two decimal places, they might be 2.20 and 1.33. NB: Given that trailing zeroes are ignored by R, you need to specify the precision if mean or standard deviation ends in 0.
sprite_parameters <- set_parameters(mean = 2.20, m_prec = 2, sd = 1.32,
n_obs = 20, min_val = 1, max_val = 5)
find_possible_distribution(sprite_parameters)
#> $outcome
#> [1] "success"
#>
#> $values
#> [1] 4 4 1 1 1 1 1 4 1 2 2 4 4 2 1 2 1 1 4 3
#>
#> $mean
#> [1] 2.2
#>
#> $sd
#> [1] 1.321881
#>
#> $iterations
#> [1] 4To find more than one distribution that matches the parameters, you can use find_possible_distributions()
find_possible_distributions(sprite_parameters, 10)
#> Only 9 matching distributions could be found. You can try again - given that SPRITE is based on random number generation, more distributions might be found then.
#> # A tibble: 9 × 6
#> id outcome distribution mean sd iterations
#> <int> <chr> <list> <dbl> <dbl> <dbl>
#> 1 1 success <dbl [20]> 2.2 1.32 8
#> 2 2 success <dbl [20]> 2.2 1.32 2
#> 3 3 success <dbl [20]> 2.2 1.32 3
#> 4 4 success <dbl [20]> 2.2 1.32 4
#> 5 5 success <dbl [20]> 2.2 1.32 4
#> 6 6 success <dbl [20]> 2.2 1.32 3
#> 7 7 success <dbl [20]> 2.2 1.32 1
#> 8 8 success <dbl [20]> 2.2 1.32 1
#> 9 9 success <dbl [20]> 2.2 1.32 4They can then be plotted to identify features that are shared across distributions.
res <- find_possible_distributions(sprite_parameters, 10)
#> Only 9 matching distributions could be found. You can try again - given that SPRITE is based on random number generation, more distributions might be found then.
plot_distributions(res)
#> Warning: Removed 18 rows containing missing values or values outside the scale range
#> (`geom_bar()`).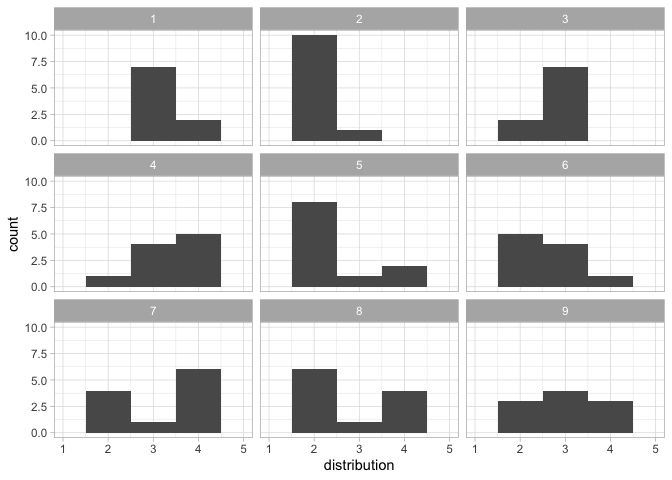
Advanced features
Multi-item scales
Often, several Likert-type items are averaged to measure a single construct (e.g., participants might be asked how happy, satisfied and fulfilled they are, with the results averaged into a measure of well-being). Possible resulting distribution can be explored by rsprite2 by specifying the n_items parameter.
sprite_parameters <- set_parameters(mean = 1.95, sd = 1.55, n_obs = 20,
min_val = 1, max_val = 5, n_items = 3)
find_possible_distribution(sprite_parameters)
#> $outcome
#> [1] "success"
#>
#> $values
#> [1] 4.333333 1.000000 1.000000 1.000000 5.000000 1.000000 5.000000 4.333333
#> [9] 1.000000 1.000000 1.000000 1.000000 3.000000 1.000000 3.333333 1.000000
#> [17] 1.000000 1.000000 1.000000 1.000000
#>
#> $mean
#> [1] 1.95
#>
#> $sd
#> [1] 1.549476
#>
#> $iterations
#> [1] 49Restrictions
Sometimes, you might know how often certain values should appear in the distribution. Such restrictions need to be passed to the set_parameters() function as a named list. They can either specify the exact number of occurrences (restrictions_exact) or the minimum number of occurrences (restrictions_minimum) of a specific value.
sprite_parameters <- set_parameters(mean = 1.95, sd = 1.55, n_obs = 20,
min_val = 1, max_val = 5, n_items = 3,
restrictions_exact = list("3"=0, "3.67" = 2),
restrictions_minimum = list("1" = 1, "5" = 1))
find_possible_distribution(sprite_parameters)
#> $outcome
#> [1] "failure"
#>
#> $values
#> [1] 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000 4.000000
#> [9] 1.000000 1.000000 1.000000 4.333333 1.000000 1.000000 1.000000 4.333333
#> [17] 1.000000 5.000000 3.666667 3.666667
#>
#> $mean
#> [1] 1.95
#>
#> $sd
#> [1] 1.511264
#>
#> $iterations
#> [1] 20000
